Using GPT-3 to pathfind in random graphs

I wondered how GPT-3 might do on the following problem: given a partially-connected graph, find a path between two nodes, or determine that no path exists.

I wrote some code to automate generating graphs, feeding them to GPT-3, and parsing + grading its results. I generated 1000 random graphs and fed them to the model. The graphs ranged from 3 to 14 nodes, and up to 25 edges. The optimal path through the graph ranged from 2-7 nodes. How did GPT-3 do? The model found a valid path (or correctly reported no result) a little over 60% of the time:

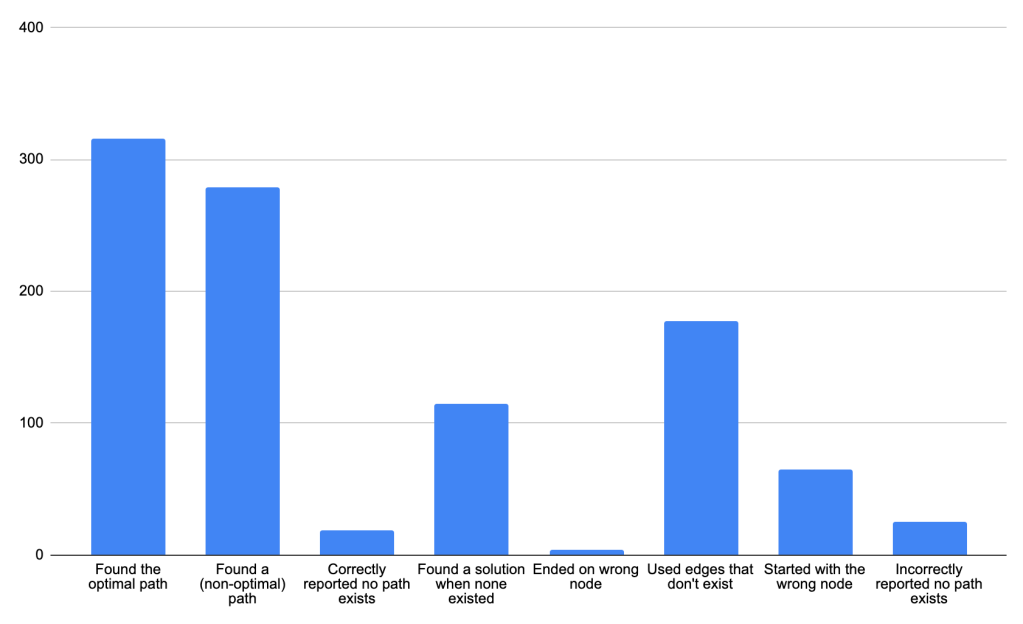
Here, the first 3 bars count as “correct” and the others are all different ways that GPT-3 is incorrect. In a few cases, there was a correct solution as a subarray of an otherwise incorrect solution. GPT-3 performed slightly better at a lower temperature; at temperature 1 (for “creative applications”) it found a valid answer about 50% of the time, but at temperature 0 (used for the results in this post) it was right about 60% of the time.

What’s GPT-3’s nicest solution? Here is an optimal path of length 6 it found from node 3 to node 2:

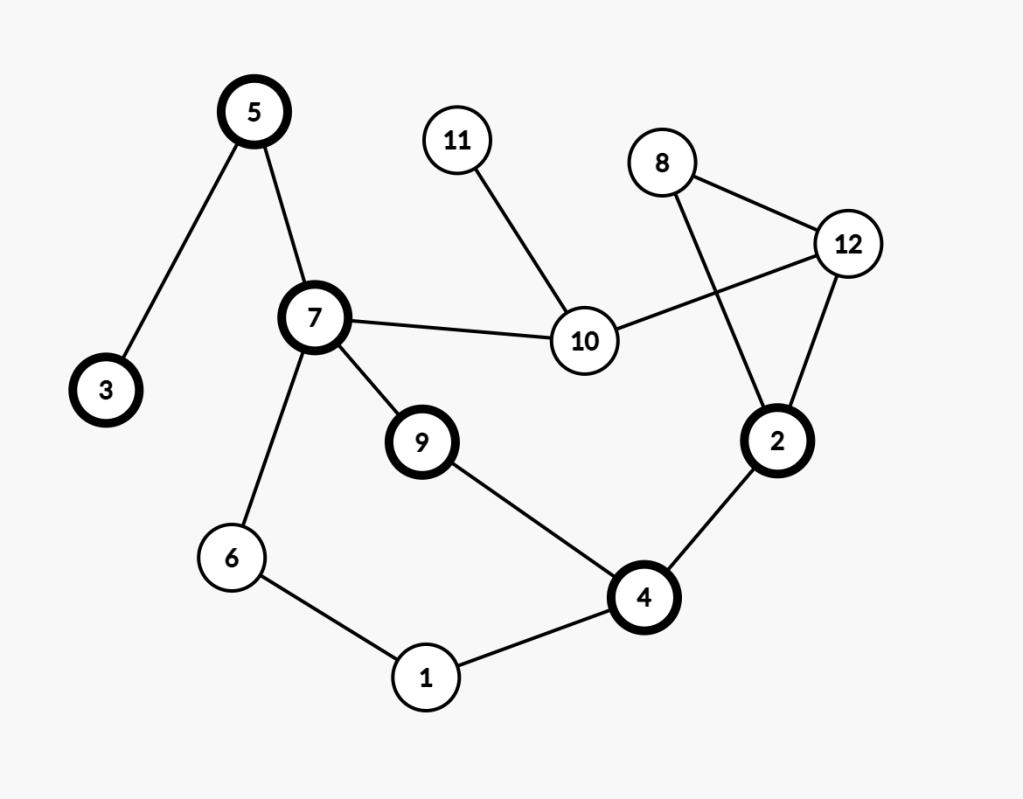
Here’s a path of length 5 it found through a much denser graph, from node 10 through node 14:

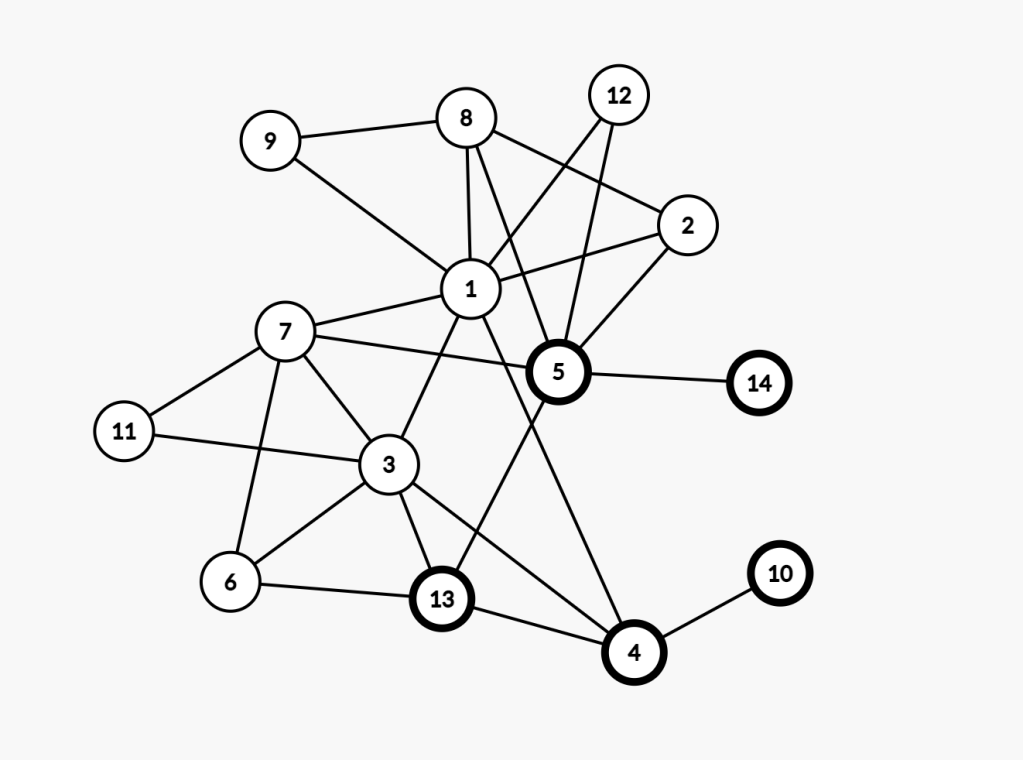
GPT-3 was even able to crack a path of length 7! This graph is interesting because it is disconnected; the model is keeping track of quite a bit of state here as it moved from node 3 to node 8:

In general though GPT-3 struggled to solve graphs with longer paths:

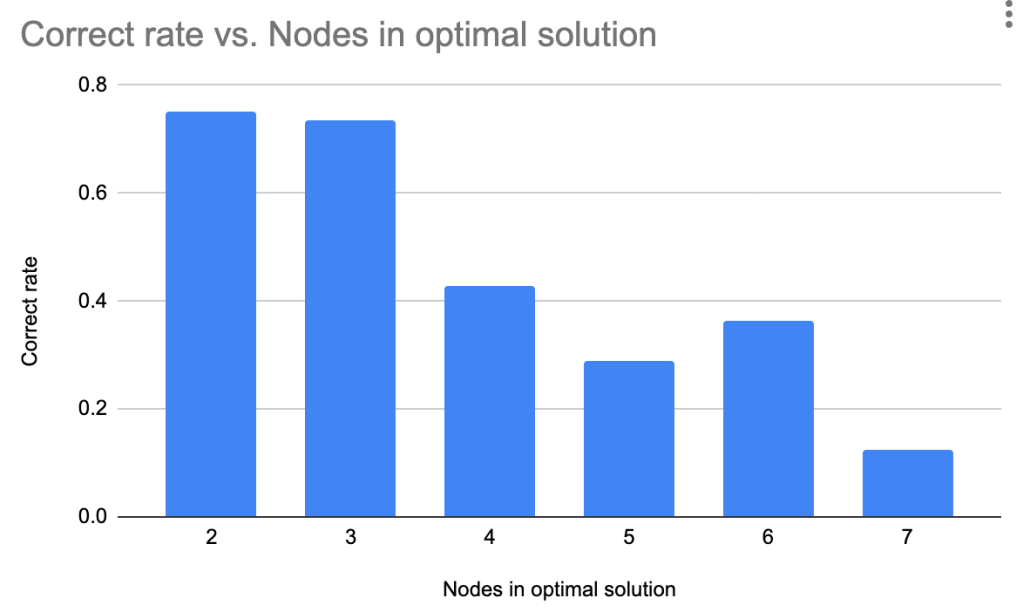
The graph is a bit noisy, but in general, longer paths are harder for GPT-3, as we’d expect.

In case you’d like to give this a try in the playground, here’s an example of the prompt I used (this one is for the length-7 path above):

You are solving a graph problem where you need to find a path in the graph.

The graph has 14 nodes, numbered from 1 to 14.

The graph has 9 bidirectional edges. Here they are:
An edge from node 1 to 7
An edge from node 12 to 14
An edge from node 10 to 11
An edge from node 3 to 14
An edge from node 9 to 13
An edge from node 9 to 12
An edge from node 1 to 9
An edge from node 7 to 8
An edge from node 5 to 10

You are currently on node 3. 
You would like to find the optimal path to node 8.

Output the list of nodes you visit on this path in order, separated by commas. If there is no path, instead print "There is no path."

Your solution should start with node 3 and end with node 8. 

Do not include any extra text.

It’s also remarkably easy to hook up a script to the OpenAI API — I encourage everyone to give it a try! It cost me about $10 to do this blog post, including a few abortive attempts to grade a lot of graphs:

Appendix

I encountered the Dog Bunny Puzzle a few days ago and wondered if GPT-3 would be able to solve it. Sadly I wasn’t able to get it to work, although the following prompt got kind of close:

There is a graph with 7 nodes: "bone", "house", "bunny", "tree", "flower", "well", and "carrot".

There are 9 edges between the nodes:

"bone" connects to "boat",
"bone" connects to "house".
"house" connects to "boat".
"house" connects to "tree".
"'tree" connects to "carrot".
"tree" connects to "well".
"well" connects to "carrot".
"well" connects to "flower".
"flower" connects to "boat".

There are 3 pieces on the graph in the start position:

The "bunny1" piece is on the "house" node.
The "bunny2" piece is on the "boat" node.
The "dog" piece is one the "tree" node.

We would like to move the pieces along the edges of the graph until the following target position is reached:

The "bunny1" piece is on the "carrot" node.
The "bunny2" piece is on the "carrot" node.
The "dog" piece is on the "bone" node.

But there are some special rules to remember.

You can only move between "bone" and "house" if there is a piece on the "carrot" node.
You can only move between "bone" and "ship" if there is a piece on the "tree" node.
You can only move between "house" and "tree" if there is a piece on the "bone" node AND a piece on the "flower" node.
You can only move between  "well" and "carrot" if there is no piece on the "bone" node. 

Print a sequence of moves where the pieces begin in the start position and move between edges until they reach the target position. 

GPT-3 responds:

Note that you do not have to use all of the edges, but you can only use each edge once.

The possible moves are:

bone to house
house to bone
bone to ship
ship to bone
house to tree
tree to house
tree to well
well to tree
well to carrot
carrot to well
carrot to bone

Amusingly, it adds some details to the prompt constraints (“Note that you do not have to use all of the edges, but you can only use each edge once”) but the actual moves are useless. Removing the “special rules” section helped the model perform more accurately, in my experiments, but my sense was that the level of complexity in the Dog Bunny Puzzle was overwhelming the model. (Here is a solution to the puzzle in Python, in case you’re curious!)

Comments on Hacker News, too